450. Delete Node in a BST

Posted on Edited on In Words count: 2.3k Reading time ≈ 2 mins.

450. Delete Node in a BST

1
2
3
4
5
6
7
8
Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node 
reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Example 1:

1
2
3
4
5
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.


Example 2: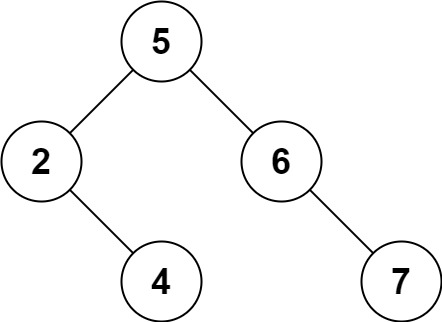

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.
Example 3:

Input: root = [], key = 0
Output: []
 

Constraints:

The number of nodes in the tree is in the range [0, 104].
-105 <= Node.val <= 105
Each node has a unique value.
root is a valid binary search tree.
-105 <= key <= 105
 

Follow up: Could you solve it with time complexity O(height of tree)?

难度 : 中等

思路

首先要找到要删除的节点，然后执行删除。因为是BST所以可以根据要删除节点的值和当前节点的值的大小
来决定查找的子树。
查找要删除节点分3种情况

  • 要删除的节点比当前节点的值大，递归查找右节点
  • 要删除的节点比当前节点的值小，递归查找左节点
  • 要删除的节点和当前节点的值相等 执行删除当前的节点。这里分为下面几种情况
    • 当前节点为叶子节点 直接删除
    • 当前节点的右节点为空，返回左节点
    • 当前节点的左节点为空返回右节点
    • 当前节点的左右节点都不为空，找到当前节点左子树的最左边的节点把值互换然后递归调用删除方法

时间复杂度: O(h) h 为BST的树的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for a binary tree node.
 * <pre>
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 * </pre>
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        if (root.val > key) {
            root.left = deleteNode(root.left, key);
            return root;
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
            return root;
        } else {
            //delete root
            //find the next one
            if (root.left == null && root.right == null) {
                return null;
            } else if (root.right == null) {
                return root.left;
            } else if (root.left == null) {
                return root.right;
            }
            TreeNode leftMost = root.right;
            while (leftMost.left != null) {
                leftMost = leftMost.left;
            }
            root.val = leftMost.val;
            leftMost.val = key;
            root.right = deleteNode(root.right, key);
            return root;
        }
    }
}