2251. Number of Flowers in Full Bloom

Posted on In Words count: 1.7k Reading time ≈ 2 mins.

2251. Number of Flowers in Full Bloom

1
2
3
4
5
6
7
8
You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in 
full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array persons of size n, 
where persons[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when 
the ith person arrives.

Example 1:


1
2
3
4
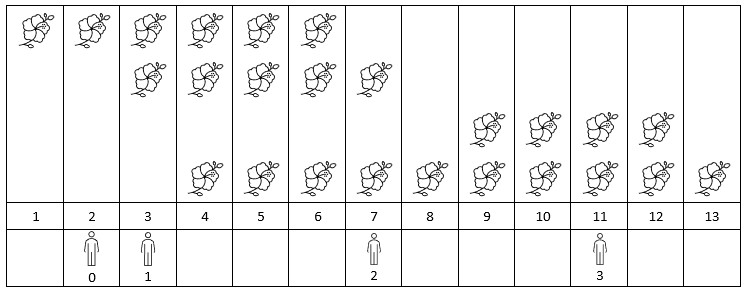
5
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
Example 2: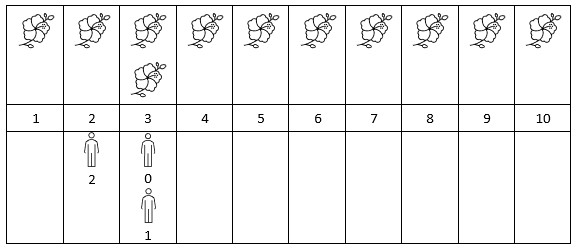


1
2
3
4
5
6
7
8
9
10
11
12
13
Input: flowers = [[1,10],[3,3]], persons = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
 

Constraints:

1 <= flowers.length <= 5 * 104
flowers[i].length == 2
1 <= starti <= endi <= 109
1 <= persons.length <= 5 * 104
1 <= persons[i] <= 109

Difficulty : Hard

Solution

Prefix sum + binary search

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] fullBloomFlowers(int[][] flowers, int[] persons) {
        TreeMap<Integer,Integer> map = new TreeMap<>();
        for (int[] flower : flowers) {
            int s = flower[0];
            int e = flower[1];
            map.put(s, map.getOrDefault(s, 0) + 1);
            map.put(e + 1, map.getOrDefault(e + 1, 0) - 1);
        }
        int sum = 0;
        for (Integer key : map.keySet()) {
            sum += map.get(key);
            map.put(key, sum);
        }
        
        int[] ans = new int[persons.length];
        for(int i = 0; i < persons.length; i++) {
            Integer key = map.floorKey(persons[i]);
            ans[i] = key != null ? map.get(key) : 0;
        }
        return ans;
        
    }
}