2360. Longest Cycle in a Graph

Posted on In Words count: 2.7k Reading time ≈ 2 mins.

2360. Longest Cycle in a Graph

1
2
3
4
5
6
7
8
9
10
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.



Example 1:


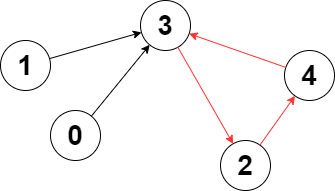
1
2
3
4
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:


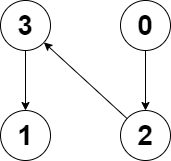
1
2
3
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

1
2
3
4
- n == edges.length
- 2 <= n <= 105
- -1 <= edges[i] < n
- edges[i] != i

Difficulty : Hard

Solution

  • int[] timeVisited = new int[n] : Create an array timeVisited of size n to store the visit sequence for each node.

  • int time = 1: Initialize a variable time to store the current visit sequence, starting from 1.

  • int ans = -1: Initialize the answer variable as -1. It will store the length of the longest cycle found.

  • Iterate through all nodes in the graph with the loop for (int i = 0; i < n; i++).

  • Check if the current node i is visited. If yes, skip the current iteration: if (timeVisited[i] > 0) continue;.

  • Initialize a variable startTime equal to the current time. This variable will store the visit sequence value when the traversal started for node i.

  • Create a loop using int j = i; and while (j != -1 && timeVisited[j] == 0) to traverse the graph along the directed edges starting from the current node i. The loop stops when it reaches a node with no outgoing edges (edges[j] == -1) or when it encounters a previously visited node (timeVisited[j] != 0).

  • Inside the loop, update the timeVisited array for the current node j with the current time value and increment time by 1: timeVisited[j] = time++;.

  • Move to the next node in the graph: j = edges[j];.

  • After the loop, check if the traversal ended on a previously visited node that was visited after the startTime. If yes, calculate the length of the cycle as time - timeVisited[j] and update the ans variable with the maximum value between the previously stored answer and the newly calculated cycle length: if (j != -1 && timeVisited[j] >= startTime) { ans = Math.max(ans, time - timeVisited[j]); }.

  • After completing the outer loop, return the answer variable ans, which stores the length of the longest cycle in the graph. If no cycles are found, it will return -1 as initialized.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int longestCycle(int[] edges) {
        int n = edges.length;
        int[] timeVisited = new int[n];
        //to simulate the visit time
        int time = 1;
        int ans = -1;
        for (int i = 0; i < n; i++) {
            if (timeVisited[i] > 0) {
                continue;
            }
            int startTime = time;
            int j = i;
            while (j != -1 && timeVisited[j] == 0) {
                timeVisited[j] = time++;
                j = edges[j];
            }
            if (j != -1 && timeVisited[j] >= startTime) {
                ans = Math.max(ans, time - timeVisited[j]);
            }
        }
        return ans;
    }
}